Computerized Ionospheric Tomography (CIT)
- Tomographic imaging of the ionosphere using GPS data.
- Computerized Ionospheric Tomography (CIT) is a method to reconstruct ionospheric electron
density image by computing Total Electron Content (TEC) values from the recorded GPS signals. Due to the multi-scale
variability of the ionosphere and inherent biases and errors in the computation of TEC, CIT constitutes an
underdetermined ill-posed inverse problem.
- Estimation of electron density distribution in the ionosphere as a function of space and time
is a problem with important application areas. GPS satellites and receivers provide Total Electron Content (TEC)
measurements along a network of lines connecting satellites to the receivers. Therefore, a line-projection relates the
electron density distribution to the available measurements resulting in a tomographic set up for the estimation
problem. However, the classical tomographic reconstruction techniques fail to provide reliable results with the limited
number of available line-projections. In addition, the time varying nature of the electron density distribution creates
further complications.
- Ionospheric imaging of electron density distribution has four dimensions in Latitude,
Longitude, Height, Time.
- Computerized Ionospheric Tomography is of utmost interest recent years. Various approaches for
the solution of the CIT include serial expansion of electron density into two dimensional basis functions, iterative
algebraic reconstruction methods, neural network and statistical analysis methods.
- For basis function expansion, the following bases can be chosen:
- Squeezed Legendre Polynomials
- Truncated Legendre Polynomials
- Haar Wavelets
- SVD based basis functions
- Optimum number of basis functions are determined by computing the error in the reconstruction.
- Tomographic reconstruction algorithms are
- Regularized Least Squares (RLS)
- Needs regularization
- Requires matrix inversion and matrix
multiplication, thus higher computational complexity compared to other techniques
- Total Least Squares (TLS)
- No regularization
- Requires SVD computation
- Useful for linear system equations,
Ax=b, in which A and b include error
- Method for regularization of ill-posed
linear Least Squares problem
- Requires SVD computation
- Algebraic Reconstruction Technique (ART)
- Iterative algorithm and independent of
basis functions
- Performance is very sensitive to the
initial state
- Hybrid Reconstruction Technique (HART)
- Initial state is obtained by TLS and
iterative ART is used for reconstruction
- No regularization is needed
- Lower reconstruction error than TLS
alone
- More efficient in implementation, lower
computational complexity
IONOLAB Contributions :
- Tomographic reconstructions of 2-D IRI based
surfaces are obtained using Basis Function Expansion (BFE) method using
- Squeezed Legendre Polynomials
- Truncated Legendre Polynomials
- Haar Wavelets
- SVD based basis functions
- RLS, TLS, TSVD, ART and HART are implemented and
performances are compared over 2-D IRI surfaces.
- It is observed that SVD bases provides
an optimum basis both for latitude and height with minimum number of basis functions to represent the variations.
- Determination of the initial state for
algebraic reconstruction techniques is of extreme importance in the convergence and reduction of reconstruction error.
- Tomographic Imaging with Random Field Priors
- CIT is performed by using a Bayesian
approach with Gaussian random field priors.
- The electron density distribution can
be estimated by the minimum mean squared error algorithm given the prior distribution of the random field and the
measurements
- The 3-D mean and the covariance of the
assumed Gaussian random field priors can either be obtained from ionospheric models such as IRI or they can be
estimated by an iterative algorithm from the GPS measurements.
- Given sparse and non-uniform TEC measurements,
the electron field is obtained from mean square estimation where the Gaussian random field structure provides
regularization.
- Geographical and temporal variations of
ionosphere can be observed by obtaining tomographic reconstructions of electron density distribution from Earth-based
GPS stations for both quiet and disturbed days of ionosphere.
- 2-D slices that will be obtained from 3-D
reconstructions can be compared with the model based reconstructions or with the available Global Ionospheric Maps from
IGS centers.
- The random field theory is applied to the
ionospheric electron density reconstruction problem for the first time and the field is estimated using the minimum
mean squared error algorithm.
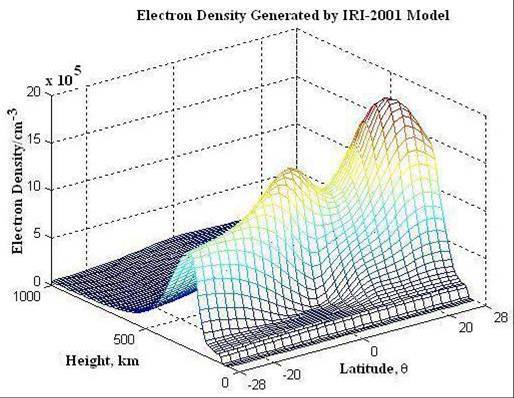
Figure 5.1 IRI Image of Ionospheric Electron Density in Latitude and Height
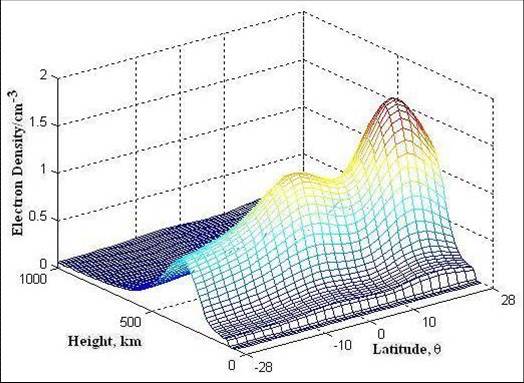
Figure 5.2 Ionospheric electron density is reconstructed with RLS and SVD basis functions both
in height and latitude. Normalized reconstruction error for 3 SVD basis both in latitude and height is epsilon (3,3) =
0.1934
- SVD Based Tomographic imaging
- In this work, to improve the reliability of the
obtained 3-D estimates, we propose an SVD based tomographic reconstruction technique, where the IRI-2001 model is used
as an a priori source of information.
- To improve the performance of the estimation, we
form the SVD basis by using IRI-2001 model results for the location and the time of interest. Also, to account for
variation as a function solar activity, we consider IRI-2001 model results with similar sun-spot number index.
- We investigated variations in the obtained SVD
basis as a function of spatial and temporal location in detail showing that there is significant change with respect to
both variables. Therefore, a reconstruction based on a fixed basis would have limited applicability around the earth.
- We also investigated reconstruction quality of
the proposed technique both on synthetic and real measurements showing that robust estimation of the ionospheric
electron density distribution that fits to the observed data as well as the IRI-2001 model is possible.
- Scientific and Technical Research Council of
Turkey, TUBITAK EEEAG 105E171: Computer Imaging of Electron Distribution Using GPS Measurements, Jun. 2006 - Jun.
2008.
- O. Arikan, F. Arikan, C.B.Erol, `3-D Ionospheric
Tomography with Random Field Priors,' in Mathematical Methods in Engineering, K. Tas, J.A. Tenreiro Machado and D.
Baleanu (Eds), Springer, Netherlands, 335-334, 2007.
- O. Arikan, F. Arikan, and C.B. Erol,
`Computerized ionospheric tomography with the IRI model', Journal of Advances in Space Research,
doi:10.1016/j.asr.2007.02.078
- E. Yavuz, F. Arikan,, O. Arikan, ve C.B. Erol,
`Model Based Comparison of Basis Functions and Reconstruction Algorithms in Computerized Ionospheric TomographyÇ, (in
Turkish) Symposium of Signal Processing and Applications, (13. Sinyal I{\c sleme and Uygulamalari Kurultayi) SIU
2005, Erciyes University, Kayseri, 16-18 May 2005.
- E. Yavuz, F. Arikan, O. Arikan, `A Hybrid
Reconstruction Algorithm for Computerized Ionospheric TomographyÇ, Proceedings of RAST-2005, Recent Advances in Space
Research, Harbiye Askeri Muze, Hava Harb Okulu, Istanbul, Turkey, 782-787, 9 - 11 June 2005.
- E. Yavuz, O. Arikan, F. Arikan, C.B. Erol,
`Computerized Ionospheric Tomography with the IRI ModelÇ, Abstracts Booklet of IRI-2005, Observatori de l'Ebre,
Roquetes, Spain, 41, 27 June - 1 July 2005.
- E. Yavuz, F. Arikan, O. Arikan and C.B. Erol,
`Algorithms and Basis Functions in Tomographic Reconstruction of Ionosphere Electron DensityÇ, Proceedings of
EUSIPCO'2005, 13th European Signal Processing Conference, Antalya, Turkey, 4-8 September 2005.
- O. Arikan, F. Arikan and C.B. Erol, `3-D
Ionospheric tomography with random field priorsÇ, Abstract Booklet of MME'06, Mathematical Methods in Engineering,
Cankaya University, Ankara, 27-29 April 2006.
- O. Erturk, O. Arikan, F. Arikan,
`Tomographic Reconstruction of the Ionospheric Electron Density as a function of Space and TimeÇ, Abstracts Booklet of
IRI/COST 296-2007, Institute of Atmospheric Physics, Prague, Czech Republic, 10 - 14 July 2007.
|








