GPS/TEC Mapping
- Ionosphere is the layer of the atmosphere that has high electron concentration. Ionosphere has an
important affect on both HF and satellite communication systems. Due to long term and short term variations caused by the
sun, ionosphere causes errors on communication systems.
- Total Electron Content (TEC) which is a measure of the total number of electrons along a path of the
radio wave can be used to further investigate the ionospheric variability. TEC is defined as the number of free electrons
along the ray path above one square meter on the ionosphere and its unit is represented as TECU (1 TECU = 1016 el/m2). TEC
measurements can be derived from the delay of the traveling time of the signals transmitted from the Global Positioning
System (GPS) satellites and recorded at the earth-based receivers. Due to a lack of a complete forward ionospheric model,
and sparse and/or irregular distribution of GPS receivers, TEC cannot be directly estimated everywhere on the
ionosphere.
- Due to the high variability of the ionosphere in space and time, the electron density distribution and
TEC can be regarded as spatiotemporal random functions similar to their counterparts in geostatistics, hydrology,
meteorology and environmental sciences. The Global Positioning System (GPS), due to its availability for civilian use in the
last 10 years, provides a cost-effective means for estimating TEC. Since GPS-TEC can be estimated only for a limited and
mostly sparsely distributed number of receiving stations, a suitable interpolation both in space and time representing the
nature of ionosphere is necessary.
- IONOLAB-TEC is a regularized estimation algorithm which combines signals from all GPS satellites for a
given instant and a given receiver for a desired time period or for 24 hours with 30 s time resolution.
- IONOLAB-TEC can be used for all latitudes and both calm and disturbed days robustly.
- Time varying local TEC maps can be obtained by the joint use of signals registered by the receiver
network.
- Interpolation techniques such as Spherical Harmonics, Kriging, Multiquadric Function Fitting, Inverse
Distance Weighting and Neural Networks are used to map the TEC, globally or regionally from the limited measurements.
IONOLAB Contributions
- Neural Networks for Ionospheric Mapping
- In addition to Kriging, Multiquadric, Spherical Harmonics
and Thin Plate Spline Interpolation, one other promising technique in Ionospheric TEC Mapping is the Neural Networks (NN)
approach.
- Due to fact that NN is well known universal function
approximator, it is frequently used in estimation and prediction for the cases where the nature of the given data is not
well defined. By using this fact and nonlinear function approximation capability of NN, random and nonlinear structure of
the ionosphere are being considered under the frame of NN models.
- Multilayer Perceptron (MLP) and Radial Basis Networks (RBN)
are applied to investigate the ionosphere mapping potential of these non-linear structures.
- The performances of these methods are tested by using
artificial surfaces which are chosen to represent probable ionosphere distributions and an IRI surface for a predetermined
time interval.
- Producing artificial data focused on two basic factors:
surface type and sampling pattern in a certain region. Different types of surfaces based on plane, exponential, gaussian,
sombrero and sinusoidal functions have been used to produce artificial ionospheric surfaces.
- Simulated surfaces are sampled by regular and irregular
sampling methods. These surfaces are sampled by using various sampling schemes under various sampling rates. MLP and RBN
learning networks are then used to reconstruct more realistic TEC distributions and resulting maps decided after a set of
tests are compared with different surfaces.
- Besides analyzing MLP and RBN capabilities over ionosphere
mapping, we also use these simulations to investigate an optimum neural network structures as well as an optimum number of
positions of GPS stations.
- MLP and RBN models of NN are also used to interpolate TEC
distribution over various regions of the ionosphere using IRI TEC.
Kriging
- From the possible mapping techniques, Kriging is generally
used in geology and mining for ore reserve calculation from the sampled values. Kriging techniques belong to the Best Linear
Unbiased Estimator (BLUE) family and calculate the estimates by minimizing the variance of the error subject to the unbiased
constraints.
- One of the advantages of Kriging among other interpolation
methods is that it gives the estimation error variance, so the confidence intervals for the estimations can be calculated.
- Mapping with Kriging can be performed by estimating each
point in a dense regularly spaced grid from regularly or irregularly distributed samples. Kriging technique can be
implemented with certain variations with different names such as Simple, Ordinary, Universal, Indicator, Disjunctive and
Co-Kriging techniques.
- Keeping the nature of TEC and sample distribution,
Ordinary Kriging (OK) and Universal Kriging (UK) can be chosen as interpolation methods in the initial step of TEC mapping.
- Due to the inherent errors in the TEC measurement and
computation, it is better to observe the performance of Kriging over synthetic TEC surfaces generated in space and combine
them with model TEC like IRI.
- In IONOLAB studies, OK and UK methods are implemented on
synthetic data sets which are assumed to be the possible TEC distributions. These data sets are obtained by adding spatially
correlated noise to a trend function. The performance of interpolation with various surface functions, regular and irregular
sampling patterns, number of sample points and variogram fitting functions is investigated with both OK and UK methods.
- A linear plane, an exponential function, a second order
polynomial, Gauss function, Sombrero function and a combination of sinusoidal and exponential functions are used for the
trend functions in order to represent an increasing complexity in TEC distribution. Normally distributed and spatially
correlated noise is simulated by the Cholesky decomposition by using an isotropic exponential covariance function with
different variance and range parameters.
- Square, triangular, hexagonal grids are used for the
regular sampling patterns and random, inhibited, clustered sampling patterns are used for the irregular sampling patterns.
For each sampling pattern, the sample numbers are chosen such that the 5%, 10%, 15%, 30%, %50 of the total points to
estimate are sampled.
- The normalized errors and maximum relative errors indicate
that triangular sampling pattern is the most efficient in the regular sampling patterns, and the inhibited sampling pattern
is the most efficient among the irregular sampling pattern types. It is observed that, as the number of samples increase,
the normalized interpolation errors of the plane, exponential and second order polynomial trend functions decrease faster
than the normalized errors for the other trend functions.
- Kriging preprocesses the data to infer the structure of
variability of the random function and when joined with the Kalman Filter, it presents an important alternative for
space-time interpolation.
- Spatiotemporal interpolation techniques implemented on TEC
estimates computed from GPS observations both in space and time by using mean and covariance functions derived from IRI-2001
and GIM.
- Regional TEC maps are generated by space-time Kriged-Kalman
technique, using both the TEC computations at the ionospheric piercing points and the regulated TEC above the receiver
stations.
- Appropriate sampling pattern and number of stations, the
optimum Kriging algorithm with the covariance function that best represents various ionospheric distributions are
determined. The estimated GPS-TEC data is used in the selected Kriging algorithm to generate regional TEC maps with
increased accuracy, reliability and space-time resolution.
- For ionospheric mapping, the range and standard deviations
of the covariance functions can be obtained from IRI, GIM or a combination of IRI and IONEX TEC values.
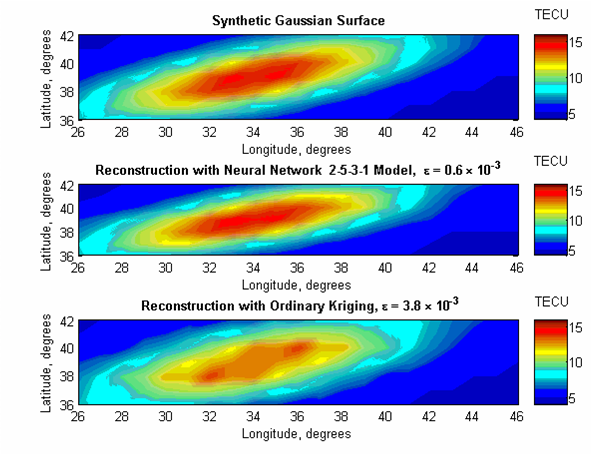
Figure 4.1 The reconstruction of a Synthetic Gaussian Surface with 7 x 21 = 147 grid points;44
uniformly sampled data points (Rectangular sampling);with Neural Network (2-5-3-1) (normalized reconstruction error, e = 0.6
10-3 );with Ordinary Kriging using Gaussian semivariogram fitting (normalized reconstruction error, e = 3.8 10-3 )
TEC Mapping with Random Field Priors
- Random Field modeling of various geological phenomena and
econometrics is a well-studied method for space-time interpolation or extrapolation. This method is applied to ionospheric
mapping for the first time in literature.
- A random field is an indexed family of random variables
which may have spatial, temporal or spatiotemporal variations. Averages and covariances of the random function in space and
time are utilized for multivariate linear estimation.
- Assuming conditional Gaussian distribution of experimental
TEC data over past TEC values, and applying Bayesian estimation, conditional posterior mean and covariance are estimated.
- In IONOLAB studies, TEC mapping with random field priors
method is implemented on synthetic data sets which are assumed to be the possible TEC distributions. These data sets are
obtained by adding spatially correlated noise to a trend function. The performance of interpolation with various surface
functions, regular and irregular sampling patterns, number of sample points and variogram fitting functions is investigated
with random field priors. In application of random field, it is assumed that the trend is given.
- A linear plane, an exponential function, a second order
polynomial, Gauss function, Sombrero function and a combination of sinusoidal and exponential functions are used for the
trend functions in order to represent an increasing complexity in TEC distribution. Normally distributed and spatially
correlated noise is simulated by the Cholesky decomposition by using an isotropic exponential covariance function with
different variance and range parameters.
- Square, triangular, hexagonal grids are used for the
regular sampling patterns and random, inhibited, clustered sampling patterns are used for the irregular sampling patterns.
For each sampling pattern, the sample numbers are chosen such that the 5%, 10%, 15%, 30%, %50 of the total points to
estimate are sampled.
- When compared to Kriging, Random Field Priors provides the
minimum relative reconstruction error for synthetic surface interpolation and forms a lower bound in the mapping
errors.
- For ionospheric mapping, the prior mean and covariances can
be obtained from IRI, GIM or a combination of IRI and IONEX TEC values.
- Random Field Priors method is also a strong alternative for
spatiotemporal interpolation of TEC for regional mapping.
Projects:
- Scientific and Technical Research Council of Turkey,
TUBITAK EEEAG 105E171: Computer Imaging of Electron Distribution Using GPS Measurements, Jun. 2006 - Jun. 2008.
Conference Publications:
- I. Sayin, F. Arikan, O. Arikan, `Synthetic TEC Mapping
with Kriging and Random Field Priors,´ (in Turkish) Symposium of Signal Processing and Applications, (15. Sinyal Isleme
and Uygulamalari Kurultayi) SIU 2007, Anadolu University, Eskisehir, Turkey, 11-13 June 2007.
- M. Gurun, K.E. Akdogan, A. Yilmaz, `Regional Ionosphere
Mapping by Using Neural Networks,´ (in Turkish) Symposium of Signal Processing and Applications, (15. Sinyal Isleme and
Uygulamalari Kurultayi) SIU 2007, Anadolu University, Eskisehir, Turkey, 11-13 June 2007.
- I. Sayin, F. Arikan, O. Arikan, `Synthetic TEC Mapping
with Ordinary and Universal Kriging´, Proceedings of RAST-2007, Recent Advances in Space Research, Harbiye Askeri Muze,
Hava Harb Okulu, Istanbul, Turkey, 14 - 16 June 2007.
- M. Gurun, K.E. Akdogan, A. Yilmaz, `Regional TEC Mapping
with Neural Networks´, Proceedings of RAST-2007, Recent Advances in Space Research, Harbiye Askeri Muze, Hava Harb Okulu,
Istanbul, Turkey, 14 - 16 June 2007.
- I. Sayin, F. Arikan, O. Arikan, `Regional Space-Time
Interpolation of GPS-TEC with Kriging´, Abstracts Booklet of IRI/COST 296-2007, Institute of Atmospheric Physics, Prague,
Czech Republic, 10 - 14 July 2007.
- M. Gurun, K.E. Akdogan, A. Yilmaz, `Comparison of Neural
Network Structures in TEC Based Regional Ionosphere Mapping´, Abstracts Booklet of IRI/COST 296-2007, Institute of
Atmospheric Physics, Prague, Czech Republic, 10 - 14 July 2007.
|







